11.
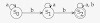
Consider the following directed graph:
The number
of different topological orderings of the vertices of the graph is ..........
Answer: 6
Explanation:
Following
are the six different topological orderings.
a-b-c-d-e-f
a-d-e-b-c-f
a-b-d-c-e-f
a-d-b-c-e-f
a-b-d-e-c-f
a-d-b-e-c-f
12.
Consider the following C program.
void f(int, short);
void main()
{
int i = 100;
short s = 12;
short *p = &s;
................ ; // call to f()
}
Which one of the following expressions, when
placed in the blank above, will NOT result in a type checking error?
(A) f(s, *s) (B)
i = f(i, s)
(C) f(i, *s) (D)
f(i, *p)
Answer: D
Explanation:
Option (A)
is wrong because we are passing *s as second argument, but s is not a pointer
variable.
Option (B)
is wrong because we are trying to store the value of function f(i,s) to i, but
look at the function definition, it is void, it has no return type.
Option (C)
is wrong because of the same reason why option (A) is wrong.
13.
The worst case running times of Insertion
sort, Merge sort and Quick sort, respectively, are:
(A) Θ(n log n), Θ(n log n), and Θ(n2)
(B) Θ(n2), Θ(n2), and
Θ(n Log n)
(C) Θ(n2), Θ(n log n), and Θ(n log
n)
(D) Θ(n2), Θ(n log n), and Θ(n2)
Answer: D
14.
Let G be a weighted connected undirected
graph with distinct positive edge weights. If every edge weight is increased by
the same value, then which of the following statements is/are TRUE?
P: Minimum spanning tree of G does not change
Q: Shortest path between any pair of vertices
does not change
(A) P only (B)
Q only
(C) Neither P nor Q (D) Both P and Q
Answer: A
15.
Consider the following C program.
#include<stdio.h>
void mystery(int *ptra, int *ptrb)
{
int
*temp;
temp
= ptrb;
ptrb
= ptra;
ptra
= temp;
}
int main()
{
int
a=2016, b=0, c=4, d=42;
mystery(&a, &b);
if
(a < c)
mystery(&c, &a);
mystery(&a,
&d);
printf("%d\n", a);
}
The output of the program ...............
Answer: 2016
Explanation:
In this
program the function swaps the pointers only, not the values in the pointers.
So the printf function will print the original value of a, which is 2016.
If we use
the below function, then it will swap the values.
void
mystery(int *ptra, int *ptrb)
{
int temp =
*ptrb;
*ptrb
= *ptra;
*ptra
= temp;
}
16.
Which of the following languages is generated
by the given grammar?
S → aS|bS|ε
Answer: D
17.
Which of the following decision problems are
undecidable ?
(A) I and IV only (B) II and III only
(C) III and IV only (D) II and IV only
Answer: C
18.
Which one of the following regular
expressions represents the language: the set of all binary strings having
two consecutive 0s and two consecutive 1s?
(A) (0+1)*0011(0+1)*+(0+1)*1100(0+1)*
(B) (0+1)*(00(0+1)*11+11(0+1)*00)(0+1)*
(C) (0+1)*00(0+1)*+(0+1)*11(0+1)*
(D) 00(0+1)*11+11(0+1)*00
Answer: B
Explanation:
(B) is the
correct option which covers all possible cases.
Set of all
binary strings having two consecutive 0s and two consecutive 1s
Anything 00
Anything 11 Anything + Anything 11 Anything 00 Anything
(0+1)*00(0+1)*11(0+1)*+(0+1)*11(0+1)*00(0+1)*
After taking
common term outside, (0+1)*(00(0+1)*11+11(0+1)*00)(0+1)*
(A)
represents strings which either have 0011 or 1100 as substring.
(C) represents
strings which either have 00 or 11 as substring.
(D)
represents strings which start with 11 and end with 00 or start with 00 and end
with 11
19.
Consider the following code segment.
x = u - t;
y = x * v;
x = y + w;
y = t - z;
y = x * y;
The minimum number of total variables
required to convert the above code segment to static single assignment
form is ................
Answer: 10
Explanation:
In compiler
design, Static Single Assignment form (SSA) is a property of an intermediate
representation, which requires that each variable is assigned exactly once, and
every variable is defined before it is used.
In the given
code segment, there are two assignments of the variable x and three assignments
of the variable y. So we use variables x1, x2 for specifying distinct
assignments of x and y1, y2 and y3 for assignment of y. So, total number of
variables is 10 (x1,x2,y1,y2,y3,t,u,v,w,z).
Static
Single Assignment form (SSA) of the given code segment is:
x1=u-t;
y1=x1*v;
x2=y1+w;
y2=t-z;
y3=x2*y2;
20.
Consider an arbitrary set of CPU-bound
processes with unequal CPU burst lengths submitted at the same time to a
computer system. Which one of the following process scheduling algorithms would
minimize the average waiting time in the ready queue?
(A) Shortest remaining time first
(B) Round-robin with time quantum less than
the shortest CPU burst
(C) Uniform random
(D) Highest priority first with priority
proportional to CPU burst length
Answer: A







0 Comments